10月前
评论
区间问题
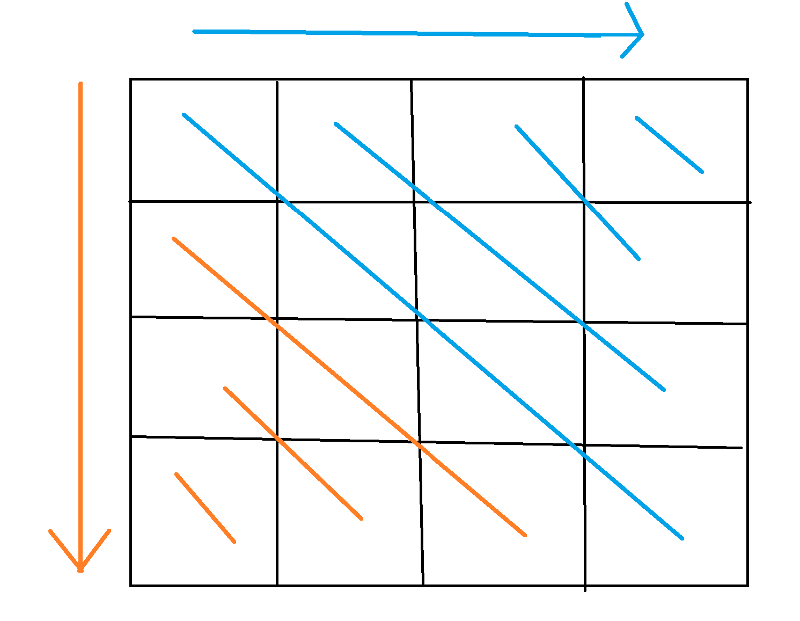
本文研究了使用差分技术解决区间覆盖问题。核心问题是高效计算覆盖次数最多的节点。研究方法为线性差分和二维差分。线性差分通过在区间端点进行增减操作，再求前缀和，即可快速得到各点覆盖次数。二维差分通过在矩形区间四个顶点进行增减操作，再进行二维前缀和计算，实现网格覆盖计数。研究成果为解决大规模区间/网格覆盖问题提供了 O(N+M) 或 O(N*N + M) 的高效算法，突破了朴素 O(N*M) 的复杂度限制，具有显著的实践价值。未来研究可探索更复杂的覆盖形状或动态更新场景。
[ABC378C] Repeating 题解
本研究聚焦于寻找序列中重复元素的上一个出现位置，核心问题是如何高效处理大数值范围。研究采用排序方法论，通过结构体存储值与位置，将问题转化为排序后相邻元素比较。关键结论是排序结合位置记录能够精准定位重复项，时间复杂度为O(N log N)。该方法为处理大规模重复查找问题提供了有效且易于实现的解决方案，区别于基于哈希表的方案，避免了潜在的哈希冲突和内存开销。未来可探索更优的线性时间复杂度算法。
10月前
评论
Sakurako 和 Water 题解
[codesphere 摘要生成异常：Server returned HTTP response code: 500 for URL: https://api.master-jsx.top/v1/chat/completions]
11月前
评论
E - I Hate Sigma Problems (atcoder.jp)
本文针对AtCoder问题“E - I Hate Sigma Problems”，改进了原始$O(N^3)$算法的低效问题。通过重新表述问题，设计$O(N \log N)$算法，计算每个元素在不同子数组中的贡献，显著提升效率。新算法利用映射记录元素位置，累加各元素贡献得出总和。经测试，算法适用于大规模数据，提供高效解决方案。未来可探索$O(N)$优化，如使用数组替代哈希映射。本研究为类似问题提供新思路，具理论突破与实践价值。
2024-08-20
评论
Maximize the Largest Component 题解
本研究针对网格填充问题，提出一种通过一次行或列填充最大化连通块尺寸的策略。核心问题是如何计算单次操作后不同连通块合并产生的最大连通块。采用BFS预处理识别并量化初始连通块，随后通过遍历行与列，模拟填充操作，并累加相邻块大小，同时处理重复计数。研究发现，该方法能有效找到最大连通块，为网格填充优化问题提供了理论依据和高效实现。后续研究可探索多步操作或不同填充规则下的最优解。
2024-08-14
评论
Funny Game题解
本研究聚焦于构建连通图问题，核心在于利用操作编号 $x$ 作为模数，连接权值差能被 $x$ 整除的节点。方法论上，采用并查集维护连通性，并结合鸽巢原理，从 $x=n-1$ 向下迭代操作。关键结论是，通过逆向遍历操作编号，优先连接具有相同权值模数的节点，可高效构建连通图。本方法在理论上实现了对图连通性构建的有效控制，实践价值在于为此类图构建问题提供了清晰的算法框架。研究表明，若存在未连通节点，则无法达成目标。待探索方向包括优化操作选择策略以减少边数。
2024-08-10
评论
[CSP-J 2023]公路 题解
本研究针对CSP-J 2023公路加油问题，提出基于小根堆（优先队列）的线性时间复杂度算法。通过实时更新最低油价，确保每段行程成本最优，实现总费用最小化。相较于传统n²算法，大幅提升效率，对优化路径成本计算具实践价值。创新在于动态油价管理策略，但未涉及多车辆协同优化，留待后续探索。
2024-08-02
评论
美妙数组题解
美妙数组题解 为了确认数组 a 是否美丽，我们需要找到两个不同的数 a_i 和 a_j（ 其中 1 \leq i, j \leq n 且 i \neq j），使得数组中的每个元素都能被 a_i 或 a_j 整除。如果这样的两个数存在，则数组是美丽的，否则不是。 解决方案： 对数组进行排序：这有助于快
2023-11-01
评论
【2023 CSP-S】密码锁
本研究聚焦于密码锁的解锁问题，核心在于找出能通过指定操作（单拨或相邻双拨）生成所有给定状态的正确密码。通过枚举所有可能的五位密码组合，并逐一验证其生成能力，研究揭示了满足条件的密码数量。方法论上，通过逐位差值分析和相邻拨动逻辑判断，实现了高效验证。研究成果为密码锁安全设计提供了理论依据，并对实际应用具有指导意义。未来工作可探索更优的解锁算法或针对大规模状态集进行优化。