Sakurako 和 Water 题解

问题概述

因为题面翻译很清楚且题面容易理解，在这里就不再解释了。

解题思路

读完题后，先看时间复杂度，再选择实现方法。一看 n\le500 ，直接 n^2 暴力就可以了。下面将具体讲解实现方法。

对角线独立处理：
- 矩阵中的每条主对角线可以单独进行操作，因为一次操作只影响一个正方形区域内的主对角线。
- 因此，可以分别计算每条对角线需要增加多少次操作。
计算每条对角线的最低高度并累加：
- 对于每条主对角线，找到其上所有位置的最低高度 min_a。更形象的可以看下面这个图，先遍历每条蓝线（橙、蓝先后顺序都可以），每条蓝线求一个最深的点存起来。橙色也同理。最后把最深的累加起来，但需要注意深度是负值，需要最后累加时取相反数。

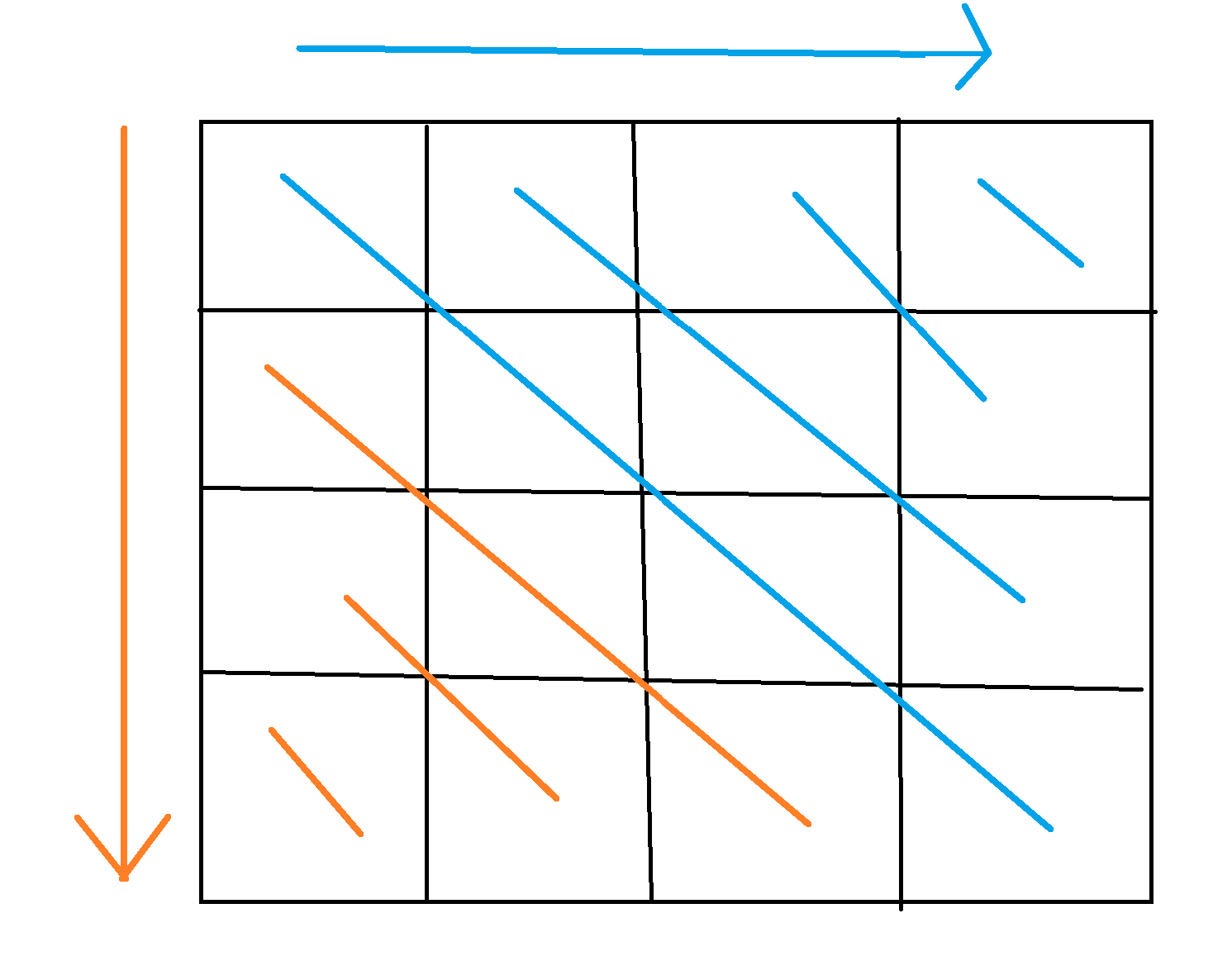
代码实现

以下是实现上述思路的代码：

#include<bits/stdc++.h>
#define ll long long
#define mem(x,y) memset(x,y,sizeof(x))
using namespace std;
const int N=1005;
int n,t,a[N][N],ans[2*N+1];
int main(){
    cin>>t;
    while(t--){
        mem(ans,0);
        mem(a,0);
        int cnt=0;
        cin>>n;
        for(int i=1;i<=n;i++){
            for(int j=1;j<=n;j++){
                cin>>a[i][j];
            }
        }
        // 遍历从第一行不同列开始的对角线
        for(int k=1;k<=n;k++){
            int i=1,j=k;
            cnt++;
            ans[cnt]=INT32_MAX; // 初始化为一个很大的值
            while(i<=n && j<=n){
                ans[cnt] = min(a[i][j], ans[cnt]);
                i++;
                j++;
            }
        }
        // 遍历从第一列不同行开始的对角线
        for(int k=2;k<=n;k++){
            int i=k,j=1;
            cnt++;
            while(i<=n && j<=n){
                ans[cnt] = min(a[i][j], ans[cnt]); //取这个对角线深度最大的那个点
                i++;
                j++;
            }
        }
        int sum=0;
        // 累加所有需要的操作次数
        for(int i=1;i<=cnt;i++){
            if(ans[i] < 0){
                sum += (-ans[i]); //注意深度是负值，需要取相反数
            }
        }
        cout<<sum<<"\n";
    }
    return 0;
}

代码说明

输入处理：
- 首先读取测试用例的数量 t。
- 对于每个测试用例，读取矩阵的大小 n，然后读取 n \times n 的高度矩阵。
遍历所有主对角线：
- 分为两部分：
  - 从第一行不同列开始的对角线：固定行 i=1，遍历列 j=1 到 j=n。
  - 从第一列不同行开始的对角线：固定列 j=1，遍历行 i=2 到 i=n。
- 对于每条对角线，找到其上的最小高度值，并存储在 ans[cnt] 中。
计算总操作次数：
- 对于每条对角线，如果其最小高度小于 0，则需要进行 -min_a 次操作。
- 将所有需要的操作次数累加，得到最终结果。
输出结果：
- 对于每个测试用例，输出计算得到的最小操作次数。

示例解析

以样例输入中的第二个测试用例为例：

2
-1 2
3 0

对角线1 (1,1) 和 (2,2) ：高度为 -1 和 0，最低高度为 -1。
对角线2 (1,2) 和 (2,1) ：高度为 2 和 3，最低高度为 2。

需要对对角线1进行 1 次操作，将其最低高度从 -1 提升到 0。对角线2不需要操作。最终输出 1。

一句话概括思路

通过将矩阵的主对角线独立处理，并计算每条对角线的最低高度，累加所有需要的操作次数，可以有效地解决此题。该方法的时间复杂度为 O(n^2)，可以通过本题。

喜欢的话不要忘记点赞哈！有任何疑问或见解欢迎在页面下方评论区发布！