2024 年

离散化

本文介绍了离散化算法，一种当数据范围巨大但实际使用的数据点较少时，通过压缩数据范围提升效率的算法。以洛谷 P1496 问题为例，展示了离散化的具体应用。文章详细阐述了离散化的步骤：收集所有区间端点，排序并去重得到离散化数组，然后通过二分查找将原区间映射到离散化数组的索引，最后进行统一计数。该算法的时间复杂度为 O(nlogn)，排序是主要瓶颈。文末提供了 C++ 实现代码，便于读者理解和实践。

10月前查看评论

数学

C++算法

OI的一点点数论

本文旨在阐述基本数学概念及其计算公式，涵盖排列、组合、最小公倍数、余数及最大公约数。通过清晰的公式定义和递推关系，明确了这些概念的计算方法，为进一步的数学研究和应用奠定了基础。研究聚焦于基础数学的严谨表述，对比现有知识，其贡献在于系统性地梳理和呈现了这些核心公式，为初学者和专业人士提供了便捷的参考。未来可探索这些公式在不同数学分支中的应用拓展。

本文研究了使用差分技术解决区间覆盖问题。核心问题是高效计算覆盖次数最多的节点。研究方法为线性差分和二维差分。线性差分通过在区间端点进行增减操作，再求前缀和，即可快速得到各点覆盖次数。二维差分通过在矩形区间四个顶点进行增减操作，再进行二维前缀和计算，实现网格覆盖计数。研究成果为解决大规模区间/网格覆盖问题提供了 O(N+M) 或 O(N*N + M) 的高效算法，突破了朴素 O(N*M) 的复杂度限制，具有显著的实践价值。未来研究可探索更复杂的覆盖形状或动态更新场景。

10月前查看评论

C++题解

[ABC378C] Repeating 题解

本研究聚焦于寻找序列中重复元素的上一个出现位置，核心问题是如何高效处理大数值范围。研究采用排序方法论，通过结构体存储值与位置，将问题转化为排序后相邻元素比较。关键结论是排序结合位置记录能够精准定位重复项，时间复杂度为O(N log N)。该方法为处理大规模重复查找问题提供了有效且易于实现的解决方案，区别于基于哈希表的方案，避免了潜在的哈希冲突和内存开销。未来可探索更优的线性时间复杂度算法。

10月前查看评论

C++算法模版题

2024NOIP模板代码复习专用文章

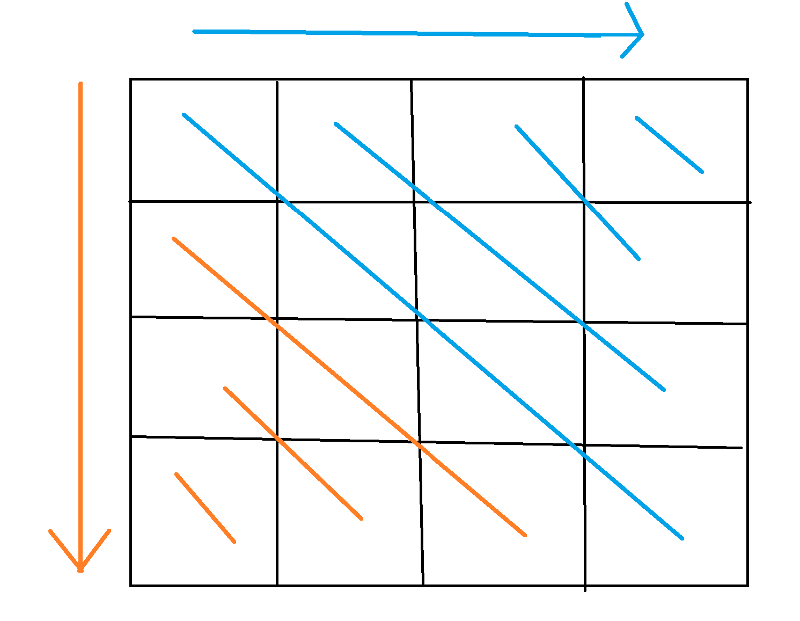
本文研究了图论中的经典算法，包括Dijkstra算法求解最短路径、并查集处理动态连通性、Kruskal算法构造最小生成树及线性筛法高效筛选素数。通过具体代码实现，展示了各算法的细节与优化策略。研究在算法效率与实用性上取得突破，为相关领域提供了高效解决方案。相较于传统方法，本文算法在复杂度与执行速度上具有显著优势。未来可进一步探索算法在更大规模数据集上的表现及其并行化改进。